Beschreibung korrelierter Vielkomponentenplasmen in kompakten Sternen und Laserplasmen
Bei der Beschreibung von astrophysikalischen Objekten wie Braunen oder Weißen Zwergen aber auch hochkomprimierten Laserplasmen (s.g. Warm Dense Matter) spielen Quanteneffekte der Elektronen eine wichtige Rolle, während die stark korrelierten Ionen häufig in guter Näherung klassisch beschrieben werden können.
Zur numerischen Untersuchung der Ionendynamik in diesen partiell ionisierten Quantenplasmen werden first-principle Molekulardynamik Simulationen durchgeführt, wobei der Einfluss der Elektronen und ihre Entartung durch dynamische Abschirmung der Ion-Ion Wechselwirkung berücksichtigt wird.
Zur Bestimmung des effektiven Ionen-Potentials wird die dielektrische Funktion in linearer Response unter Berücksichtigung von Stößen berechnet. Dadurch werden der Einfluss kollektiver Anregungen der Elektronen, Instabilitäten und Wake-Effekte berücksichtigt. Quanteneffekte der Ionen werden durch eine Renormierung ihrer Wechselwirkung auf kurzen Abständen einbezogen. Für detaillierte Darstellung siehe unsere Publikation in J. Phys. Conf. Series 220, 012003 (2010).
Anziehung 'gleich' geladener Teilchen
Elektrisch geladene Körper mit einer Ladung gleichen Vorzeichens stoßen sich ab. Dies ist natürlich allgemeingültig. In einem strömenden (komplexen) Plasma kann man jedoch beobachten, dass sich z.B. zwei negativ geladene Staubpartikel anziehen!
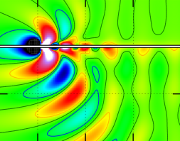
Ähnlich wie ein schnelles Boot eine Kielwelle (engl.: wake) hinter sich herzieht, erzeugen Ionen bei hoher Strömungsgeschwindigkeit ein stark oszillierendes elektrostatisches Potential hinter einem entgegengesetzt geladenen (viel größerem) Staubpartikel, wenn sie dieses umströmen. Da im 'Kielwasser' dieser Staubteilchen dabei sogar das Vorzeichen des Raumladungspotentials wechselt, können nicht nur entgegengesetzt geladene, sondern - an geeigneter Stelle - auch Teilchen mit Ladung gleichen Vorzeichens darin eingefangen werden (siehe Bildunterschrift). Eine systematische Analyse zur Struktur dieser Wakepotentiale wurde im Fachjournal New Journal of Physics veröffentlicht.
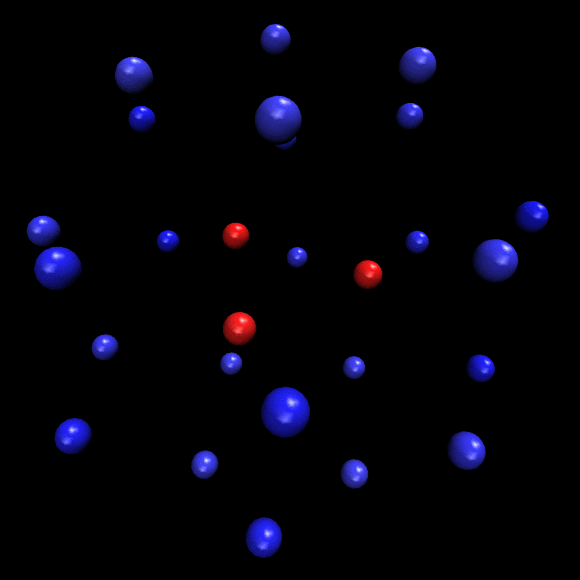
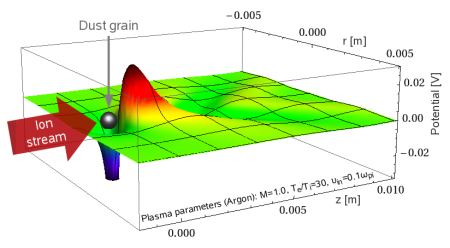 Potentiallandschaft eines negativ geladenen "Staubteilchens", das von positiv geladen (viel kleineren) Ionen mit Schallgeschwindigkeit umströmt wird. Die Ionen werden durch die vom Staubteilchen ausgehende elektrische Anziehungskraft umgelenkt und hinter diesem fokussiert. An dieser Stelle entsteht ein Gebiet mit positiver Raumladung (rot-schwarzer Bereich). Ein anderes in Strömungsrichtung befindliches (ebenfalls negativ geladenes) Staubpartikel sieht demnach eine positive Landung und wird von dieser zum anderen Staubteilchen hin angezogen! (Berechnet mit Mathematica)
Potentiallandschaft eines negativ geladenen "Staubteilchens", das von positiv geladen (viel kleineren) Ionen mit Schallgeschwindigkeit umströmt wird. Die Ionen werden durch die vom Staubteilchen ausgehende elektrische Anziehungskraft umgelenkt und hinter diesem fokussiert. An dieser Stelle entsteht ein Gebiet mit positiver Raumladung (rot-schwarzer Bereich). Ein anderes in Strömungsrichtung befindliches (ebenfalls negativ geladenes) Staubpartikel sieht demnach eine positive Landung und wird von dieser zum anderen Staubteilchen hin angezogen! (Berechnet mit Mathematica)
Simulationen zur Staubdynamik in einem strömenden Plasma sind auf der DDS-Projektseite zu finden. Bei diesen Vielteilchen-Simulationen kommen die 'Wake'-Potentiale zur Anwendung. Von vordergründigem Interesse der Untersuchung war die selbstorganisierte Strukturbildung des Staubs in Abhängigkeit von der Ionen-Strömungsgeschwindigkeit. Die Ergebnisse wurden im Fachjournal Plasma Physics and Controlled Fusion publiziert.
Schmelzkriterium für Mikro- und Nanoplasmen
Kollektives Verhalten sehr vieler Teilchen führt in großen, makroskopischen Systemen zu Ordnungsphänomenen, für die wir im Alltag Begriffe wie 'fest' (Festkörper, z.B. ein Kristall) oder 'flüssig' verwenden.
Teilt man einen Kristall in zwei Hälften, bleibt er immer noch ein Kristall. Die Frage ist nun, wie häufig kann man diese Vorgang wiederholen, bevor die Kristall-Eigenschaften verloren gehen? Und wie lässt sich der Schmelzpunkt für einen Kristall aus nur wenigen Teilchen (z.B. einige wenige Elektronen) bestimmen.
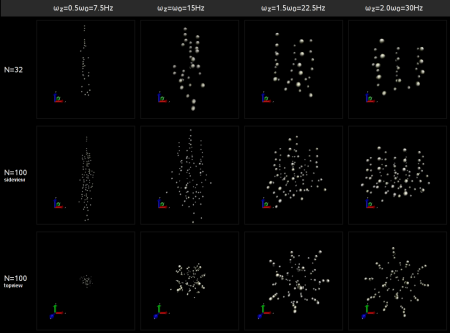
Um diese Fragen zu beantworten, musste ein neues Schmelzkriterium gefunden werden, dass sowohl in makroskopischen als auch finiten Systemen, d.h. auf sehr kleinen Skalen, funktioniert. Es beruht auf einer Verallgemeinrung des sogenannten Lindemann-Kriteriums. Dazu wird die Amplitude der relativen Abstandsfluktuationen urel von Teilchenpaaren als Funktion der Zeit gemessen. Diese Größe schwankt in der festen Phase um einen kleinen Wert (vgl. untere Zeile der Abbildung), in der flüssigen Phase um einen deutlich größeren Wert (obere Zeile). Im Übergangsbereich zeigt diese Größe ein bimodales Verhalten (rechts), aus dem sich der Schmelzpunkt bestimmen lässt.

Die Forschungsergebnisse wurden in den Physical Review Letters veröffentlicht. Der Nachweis über die experimentelle Anwendbarkeit des Kriteriums ist Jan Schablinski in seiner Diplomarbeit über 'Kontrolle von Struktur und Dynamik finiter Plasmakristalle mittels Lasermanipulation' (CAU Kiel, 2010) gelungen.
Eine Falle für stark korrelierte Exzitonen in Halbleitern
Exzitonen sind bosonische Quasiteilchen in Halbleitern. Sie entstehen, wenn Elektronen aus dem Valenzband in das Leitungsband angeregt werden und sich bei geringen Temperaturen mit dem im Valenzband zurückbleibenden Löchern über die attraktive Coulombwechselwirkung binden (siehe Abbildung). Bosonische Materie in Fallen ist von großem Forschungsinteresse in Hinblick auf einen makroskopisch besetzten Quantenzustand - dem Bose-Einstein-Kondensat. Neben dem fundamentalen Interesse an diesem noch weitgehend unerforschten Materiezustand gibt es aber auch anwendungsorientierte Motive die Zustände exzitonischer Materie zu untersuchen, denn Exzitonen bestimmen wesentlich die optischen Eigenschaften eines Halbleiters. Die kontrollierte Manipulation der exzitonischen Zustände kann die Realisierung völlig neuartiger Anwendungen in der Nanotechnologie ermöglichen. Anwendungspotential für Exzitonen als ideale Einzelphotoenquellen gibt es vorrangig in der Optoelekronik, darüber hinaus aber auch bei der Realisierung von Qbits sowie perspektivisch bei der Hochtemperatur-Supraleitung und dem Materielaser.
 Energieschema der Quantum-Well-Struktur in einem Halbleiter.
Links: Der zweidimensionale GaAs/AlGaAs Quantenfilm der Dicke L bildet ein Kastenpotential für die ins Leitungsband gepumpten Elektronen (e) bzw. die im Valenzband zurückgebliebenen Löcher (h). Rechts: Ein elektrisches Feld senkrecht zur Quantenfilmebene bewirkt eine Bandverkippung, die zur räumlichen Separation der Elektronen und Löcher führt (Bildung räumlich indirekter Exzitonen).
Energieschema der Quantum-Well-Struktur in einem Halbleiter.
Links: Der zweidimensionale GaAs/AlGaAs Quantenfilm der Dicke L bildet ein Kastenpotential für die ins Leitungsband gepumpten Elektronen (e) bzw. die im Valenzband zurückgebliebenen Löcher (h). Rechts: Ein elektrisches Feld senkrecht zur Quantenfilmebene bewirkt eine Bandverkippung, die zur räumlichen Separation der Elektronen und Löcher führt (Bildung räumlich indirekter Exzitonen).
Um kollektives Vielteilchenverhalten (Korrelationseffekte), der durch Laseranregung erzeugten Exzitonen studieren zu können, muss zunächst eine hinreichend lange Lebensdauer der Quasiteichen gewährleistet sein. Dazu ist es notwendig, Elektron und Loch räumlich zu separieren, d.h. den Überlapp ihrer Wellenfunktion und damit die spontane Rekombinationswahrscheinlichkeit zur verringern. Eine Möglichkeit dies zu realisieren ist es, die Exzitonen in einen nur wenige Nanometer dicken Quantenfilm (bezüglich der z-Richtung) einzusperren und mit einem elektostatischen Feld Ez zu polarisieren. Die räumlich indirekten Exziton sind dann senkrecht zur Quantenfilmebene ausgerichtete Dipole. Damit Exziton-Exziton-Korrelationseffekte ins Spiel kommen ist zusätzlich ein Fallenpotential in der Quantenfilmebene erforderlich, das die auseinandertreibende Dipolkraft kompensiert. Unsere Forschungsarbeit zeigt, dass eine geeignete Fallengeometrie durch das inhomogene elektrostatische Feld einer sehr feinen, elektrisch geladenen Spitze (z.B. der eines Tunnelmikroskops) durch den sogenannten "Quantum-Confined-Stark-Effekt" erzeugt werden kann. Der Vorteil einer elektrostatischen Falle für die (neutralen) Exzitonen besteht dabei in der Möglichkeit, dass die Fallenparameter und damit die Eigenschaften der exzitonischen Zustände flexibel eingestellt und kontrolliert werden können. Unsere Arbeit zur Exzitonenfalle ist in Physica Status Solidi (b) 243, No. 10, 2363 (2006) erschienen.
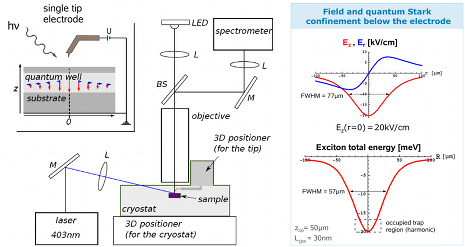 Eine elektrostatische Falle für Exzitonen
Links: Schematische Skizze des Aufbaus an der Uni Rostock. Das inhomogene elektrische Feld wird durch eine feine Spitze in den Quantenfilm induziert. Das Inset (l.o.) zeigt eine Vergrößerung der Probe.
Rechts: Feld und Fallenpotential im Quantenfilm unterhalb der Elektrode. Während der radiale Feldanteil (blau) im Fallenzentrum verschwindet, ist die z-Komponente des Feldes (rot) hier am größten. Die potentielle Energie der Exzitonen
wird am Ort der größten Feldstärke minimiert. Für Details siehe Phys. Stat. Sol. (c) 6, No. 2, 551 (2009).
Eine elektrostatische Falle für Exzitonen
Links: Schematische Skizze des Aufbaus an der Uni Rostock. Das inhomogene elektrische Feld wird durch eine feine Spitze in den Quantenfilm induziert. Das Inset (l.o.) zeigt eine Vergrößerung der Probe.
Rechts: Feld und Fallenpotential im Quantenfilm unterhalb der Elektrode. Während der radiale Feldanteil (blau) im Fallenzentrum verschwindet, ist die z-Komponente des Feldes (rot) hier am größten. Die potentielle Energie der Exzitonen
wird am Ort der größten Feldstärke minimiert. Für Details siehe Phys. Stat. Sol. (c) 6, No. 2, 551 (2009).
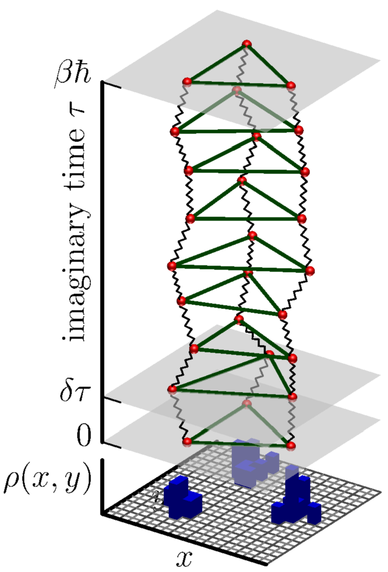
Eine direkte Lösung der Grundgleichungen der Physik für das exzitonische Vielteilchenproblem wird erst durch moderne numerische Simulationsmethoden ermöglicht. Die theoretische Beschreibung erfolgt dabei, im Gegensatz zu statistischen Methoden, von den einzelnen Elementarteilchen ausgehend (bottom up). Insbesondere der Einsatz von Pfad-Integral-Monte-Carlo-Simulationen eröffnet die Möglichkeit, das betrachtete Quantensystem mit einer Größe von bis zu einigen hundert Teilchen unter exakter Berücksichtigung aller Coulomb-Wechselwirkungs-Kräfte sowie seiner quantenstatistischen Freiheitsgrade simulieren zu können. Durch systematische Untersuchung des Einflusses des Materials und Schichtdicke des Quantenfilms, sowie der externen Kontrollgrößen wie Temperatur, Exzitonendichte und Feldstärke konnten die entsprechenden Parameterbereiche bestimmt werden, die die Chance eröffnen, in Experimenten interessante Vielteilchen-Korrelationseffekte wie z.B. Exzitonenkristalle (siehe Abbildung) und Bose-Einstein-Kondensation beobachten zu können. Da wissenschaftliche Computersimulationen, insbesondere von Quantensystemen, leicht an die Grenzen modernster Rechentechnik stoßen, ist die Entwicklung parallelisierter Codes und die Verwendung von Hochleistungsrechnen unumgänglich. Unsere theoretischen Vorhersagen und die Ergebnisse der ersten Messungen wurden in der Zeitschrift Physica Status Solidi (c) 6, No. 2, 551 (2009) veröffentlicht.
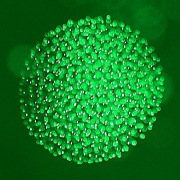
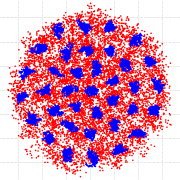
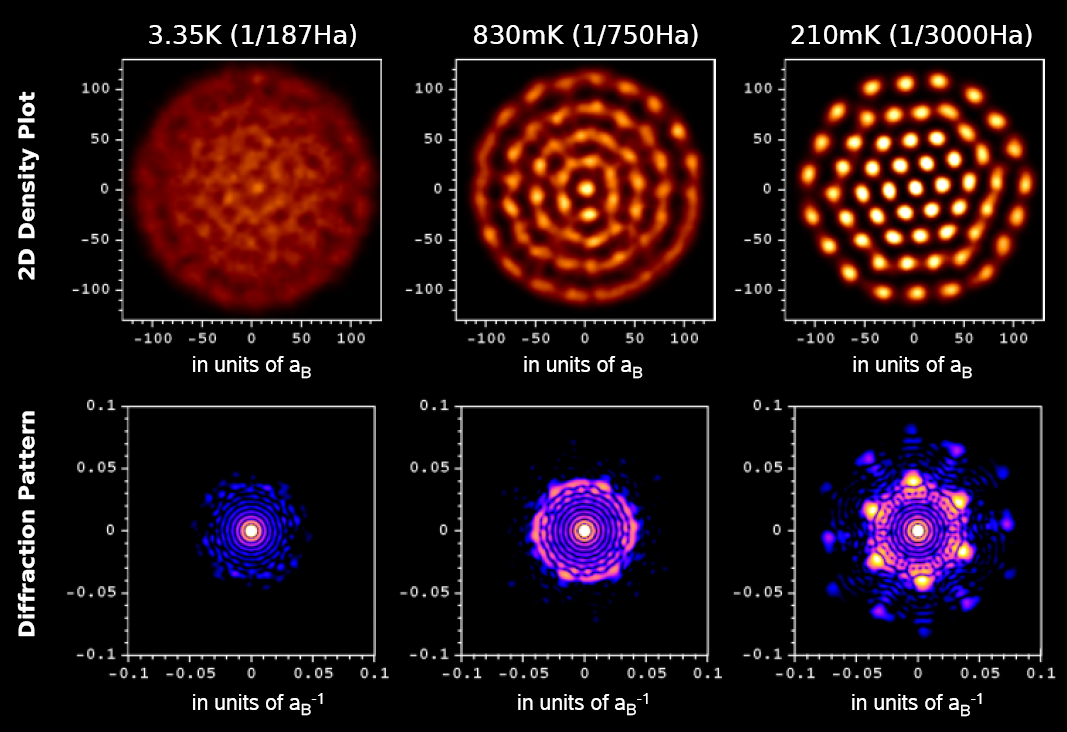 Ein Nanokristall aus Exzitonen.
Quanten-Monte-Carlo Simulation von 56 Exzitonen in einen 30nm dicken ZnSe-Quantenfilm und die Temperaturen: 3.35K (-269.8° Celsius), 830mK und 210mK.
Die Dichteverteilung der Exzitonen (oben) zeigt einen zweistufigen Kristallisationsprozess wenn eine kritische Temperatur von etwa einem Kelvin unterschritten wird: (i) Bildung einen Schalenstruktur (ähnlich einem Atom), (ii) Ausbildung eines (bosonischen) Nanokristalls mit einem hexagonalen Wigner-Gitter. Die zunehmende Lokalisierung der Teilchen erfolgt durch ausfrieren jeglicher thermischer Fluktuationen (es bleiben nur Quantenfluktuationen).
Die ausgeprägten Peaks im Beugungsbild (unten rechts) sind ein klares Indiz für einen Phasenübergang.
Ein Nanokristall aus Exzitonen.
Quanten-Monte-Carlo Simulation von 56 Exzitonen in einen 30nm dicken ZnSe-Quantenfilm und die Temperaturen: 3.35K (-269.8° Celsius), 830mK und 210mK.
Die Dichteverteilung der Exzitonen (oben) zeigt einen zweistufigen Kristallisationsprozess wenn eine kritische Temperatur von etwa einem Kelvin unterschritten wird: (i) Bildung einen Schalenstruktur (ähnlich einem Atom), (ii) Ausbildung eines (bosonischen) Nanokristalls mit einem hexagonalen Wigner-Gitter. Die zunehmende Lokalisierung der Teilchen erfolgt durch ausfrieren jeglicher thermischer Fluktuationen (es bleiben nur Quantenfluktuationen).
Die ausgeprägten Peaks im Beugungsbild (unten rechts) sind ein klares Indiz für einen Phasenübergang.